The Prisoner's Dilemma

In Game Theory, there's a famous hypothetical scenario called the Prisoner's Dilemma in which two criminal suspects are apprehended by police.

Each prisoner is in solitary confinement with no means of speaking to or exchanging messages with the other. The police admit they don't have enough evidence to convict the pair on the principal charge. They plan to sentence both to 6 months in prison on a lesser charge. Simultaneously, the police offer each prisoner a Faustian bargain. If he testifies against his partner, he will go free while the partner will get ten years in prison on the main charge. Oh, yes, there is a catch ... If both prisoners testify against each other, both will be sentenced to five years in jail.

If both suspects stay silent, they both get off with a very light sentence. If they both turn on each other, they both get a longer sentence. And if only one of them rats out the other, the suspect who squeals goes free, while the one who stayed silent receives the worst sentence.

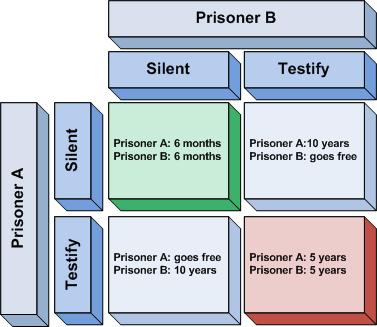
Naturally, the best choice is for both prisoners to stay silent-- they both get off with a very light sentence. 

But imagine that your accomplice is in there being interrogated. You know that he's been offered the same deal... if he rats you out, he'll go free while you take the heat. When it's your turn, would you stay silent and risk a huge prison sentence while he walks?

The scenario points to an inevitable conclusion: each prisoner rats out the other, and they both do heavy jail time. It's clearly a sub-optimal outcome, known in Game Theory as the Nash Equilibrium.